SÉRIOVÝ REZONANČNÝ OBVOD - Skolsky1
Hlavná ponuka
- REZONANCIA
- TEÓRIA
- VÝPOČTY
- DIAGRAMY
- VIDEO
- TEST
- BIBL. ODKAZY
SÉRIOVÝ REZONANČNÝ OBVOD
Tak ako v rôznych iných fyzikálnych sústavách, aj v elektrických obvodoch, vyznačujúcich sa určitými vlastnosťami, dochádza pri zhode vnútených a vlastných kmitov sústavy k výraznému zväčšeniu amplitúdy kmitov, teda k rezonančnému javu. Elektrické obvody využívajúce tento jav sa nazývajú rezonančné obvody, a túto ich vlastnosť využívame napr. na výber (detekciu) alebo potlačenie (filtráciu) napätia, resp. prúdu určitých frekvencií.
V elektrickom obvode môže dôjsť k rezonancii len vtedy, ak sa v ňom súčasne vyskytujú prvky akumulujúce elektrickú a magnetickú energiu, teda kondenzátory ( kapacitory ) a cievky (induktory ).
Najjednoduchší sériový rezonančný obvod vznikne spojením troch základných prvkov, a to odporu ( rezistora ) , kondenzátora a cievky za sebou.
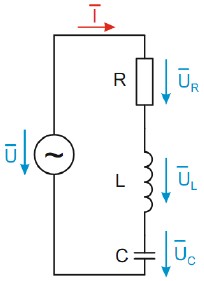
a) schéma sériového RLC obvodu
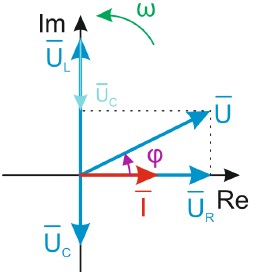
b) fázorový diagram sériového RLC obvodu
Podľa II. Kirchoffovho zákona pre fázory napätia v obvode sériového RLC obvodu pripojeného ku zdroju harmonického napätia platí:
teda
Fázor prúdu je
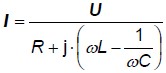
Z výrazu pre fázor prúdu a fázový diagram napätí a prúdu obvodu vyplýva, že zmenou parametrov obvodu ( C, L alebo ω ) je možné dosiahnúť stav, keď sa obvod chová ako obvod len odporom R. Podmienkou pre tento stav obvodu, ktorý označujeme ako rezonančný stav , je splnenie rovnosti
Túto podmienku možno pri konštantných hodnotách parametrov C , L splniť zmenou uhlovej frekvencie ω , pričom pre túto význačnú uhlovú frekvenciu , tzv. rezonančnú uhlovú frekvenciu ω = ωrez platí
z čoho môžeme odvodiť Thomsonov vzťah
Pri splnení rezonančnej podmienky je veľkosť napätia na cievke ( induktore ) rovnaká ako na kondenzátore ( kapacitore ) , pričom tieto napätia sú v protifáze. V rezonancii je celé napätie zdroja na odpore ( rezistore ) , pričom v obvode s malým odporom R môže byť napätie na kondenzátore a cievke omnoho väčšie ako je napájacie napätie obvodu. Prúd obvodu je v rezonančnom stave maximálny, jeho fáza je rovnaká ako fáza napätia zdroja.
Fázor prúdu je
Ak sa z praktických dôvodov zavedie pomerný prúd, je tento v komplexnom tvare
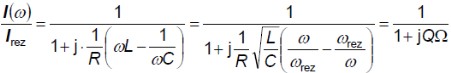
kde Q a ω sú veličiny s rozmerom 1 ( v minulosti sa používalo označenie "bezrozmerné veličiny" )
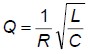
-

-
Veľkosť ( efektívna hodnota ) pomerného prúdu je
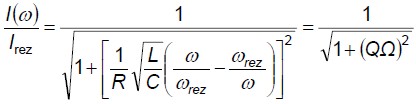
Závislosť komplexného pomerného prúdu od uhlovej frekvencie graficky zobrazíme ako amplitudovú charakteristiku, t. j. závislosť veľkosti pomerného prúdi I(f)/Irez od frekvencie f= Ω/2π
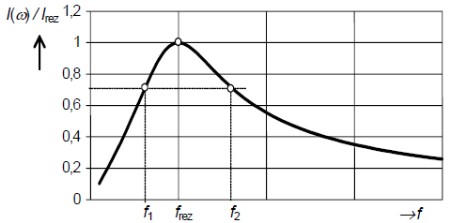
Prúd nadobúda najväčšie hodnoty v okolí rezonančnej frekvencie. Pri malých, resp. veľkých frekvenciách je prúd malý, čiže obvod sa chová ako pásmový priepust. Za pásmo priepustnosti rezonančného obvodu sa považuje interval frekvencie < f1 , f2>, v ktorom veľkosť pomerného prúdu I(f)/Irez nepoklesne pod hodnotu 1/Ѵ2 ( v obvykle používanej logaritmickej miere tomu zodpovedá pokles 20.log(1/Ѵ2) = 3 db ).
amplitudová charakteristika seriového rezonančného obvodu
Frekvencie ω1 , ω2 sa môžu určiť z podmienky
Táto podmienka vedie pre obe znamienka na kvadratické rovnice pre premennú omega, ich riešením sa určia uhlové frekvencie ω1 , ω2 , rep. frekvencie f1 a f2
čiže
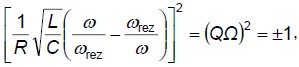

resp.
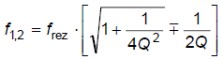
a odtiaľ pásmo priepustnosti sériového rezonančného obvodu
Faktor kvality Q priamo súvisí s pásmom priepustnosti rezonančného obvodu -
Impedanciu Z v sériovom rezonančnom RLC obvode vyjadruje vzťah :
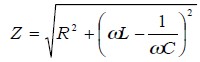
Fázový posun φ v obvode sériového RLC obvodu vyjadruje vzťah :
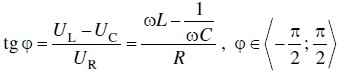
Frekvenčná závislosť relatívnej (normovanej) amplitúdy prúdu I / Io -
